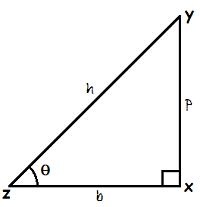
Let ∠YZX = θ in a right angled triangle XYZ.sin θ = PerpendicularHypotenuse = ph
cos θ = BaseHypotenuse = bh
tan θ = PerpendicularBase = pb
cosec θ = HypotenusePerpendicular = 1sin θ = hp
sec θ = HypotenuseBase = 1cos θ = hb
cot θ = BasePerpendicular = 1tan θ = bp
Trigonometric Identities :
sin2θ + cos2θ = 1
1 + tan2θ = sec2θ
1 + cot2θ = cosec2θ
tan θ x cot θ = 1
tan θ = sin θcos θ
cot θ = cos θsin θ
Results on complementary angles
The angles θ° and (90° − θ) are called complementary angles.sin (90° − θ) = cos θ
cos (90° − θ) = sin θ
tan (90° − θ) = cot θ
cosec (90° − θ) = sec θ
sec (90° − θ) = cosec θ
cot (90° − θ) = tan θ
Value of Trignometric Ratios
| θ | sin θ | cos θ | tan θ | cosec θ | sec θ | cot θ |
|---|---|---|---|---|---|---|
| 0° | 0 | 1 | 0 | ∞ | 1 | ∞ |
| 30° | 12 | √32 | 1√3 | 2 | 2√3 | √3 |
| 45° | 1√2 | 1√2 | 1 | √2 | √2 | 1 |
| 60° | √32 | 12 | √3 | 2√3 | 2 | 1√3 |
| 90° | 1 | 0 | ∞ | 1 | ∞ | 0 |
Sum Formulae
sin (A + B) = sin A cos B + cos A sin B.
cos (A + B) = cos A cos B − sin A sin B.
tan (A + B) = tan A + tan B 1 − tan A tan B