Aptitude - Trigonometry
1.
The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is :
Answer
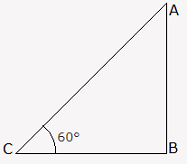 Let AB be the wall and AC be the ladder.
Let AB be the wall and AC be the ladder.
Then, ∠ACB = 60° and AC = 4.6 m.
BC AC = cos 60° = 12
⇒ AC = 2 x BC = (2 x 4.6) m = 9.2 m.
Answer :
Option DExplanation :
 Let AB be the wall and AC be the ladder.
Let AB be the wall and AC be the ladder.Then, ∠ACB = 60° and AC = 4.6 m.
BC AC = cos 60° = 12
⇒ AC = 2 x BC = (2 x 4.6) m = 9.2 m.
2.
An observer 1.6 m tall is 20√3 m away from a tower. The angle of elevation from his eye to the top of the tower is 30°. The height of the tower is :
Answer
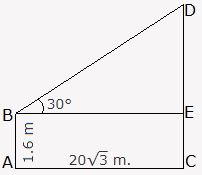 Let AB be the observer and CD be the tower.
Let AB be the observer and CD be the tower.
Draw BE ⊥ CD.
Then, CE = AB = 1.6 m, BE = AC = 20√3 m.
DEBE = tan 30° = 1√3
⇒ DE = 20√3√3m = 20 m.
∴ CD = CE + DE = (1.6 + 20) m = 21.6 m.
Answer :
Option AExplanation :
 Let AB be the observer and CD be the tower.
Let AB be the observer and CD be the tower.Draw BE ⊥ CD.
Then, CE = AB = 1.6 m, BE = AC = 20√3 m.
DEBE = tan 30° = 1√3
⇒ DE = 20√3√3m = 20 m.
∴ CD = CE + DE = (1.6 + 20) m = 21.6 m.
3.
The angle of elevation of the sun, when the length of the shadow of a tree √3 times the height of the tree, is :
Answer
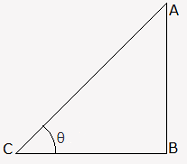 Let AB be the tree and AC be its shadow.
Let AB be the tree and AC be its shadow.
Let ∠ACB = θ
Then, AC AB = √3 ⇒ cot θ
∴ θ = 30°
Answer :
Option AExplanation :
 Let AB be the tree and AC be its shadow.
Let AB be the tree and AC be its shadow.Let ∠ACB = θ
Then, AC AB = √3 ⇒ cot θ
∴ θ = 30°
4.
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
Answer
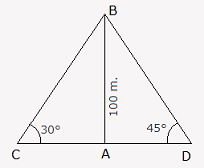 Let AB be the lighthouse and C and D be the positions of the ships.
Let AB be the lighthouse and C and D be the positions of the ships.
Then, AB = 100 m, ∠ACB = 30° and ∠ADB = 45°.
ABAC = tan 30° = 1√3 ⇒ AC = AB x √3 = 100√3 m.
ABAD = tan 45° = 1 ⇒ AD = AB = 100 m.
∴ CD = (AC + AD) = (100√3 + 100) m
= 100(√3 + 1) = (100 x 2.73) m = 273 m.
Answer :
Option CExplanation :
 Let AB be the lighthouse and C and D be the positions of the ships.
Let AB be the lighthouse and C and D be the positions of the ships.Then, AB = 100 m, ∠ACB = 30° and ∠ADB = 45°.
ABAC = tan 30° = 1√3 ⇒ AC = AB x √3 = 100√3 m.
ABAD = tan 45° = 1 ⇒ AD = AB = 100 m.
∴ CD = (AC + AD) = (100√3 + 100) m
= 100(√3 + 1) = (100 x 2.73) m = 273 m.